二叉树-BT
二叉树(Binary tree)是树形结构的一个重要类型
相关术语
- ①节点:包含一个数据元素及若干指向子树分支的信息
- ②节点的度:一个节点拥有子树的数目称为节点的度
- ③叶子节点:也称为终端节点,没有子树的节点或者度为零的节点
- ④分支节点:也称为非终端节点,度不为零的节点称为非终端节点
- ⑤树的度:树中所有节点的度的最大值
- ⑥节点的层次:从根节点开始,假设根节点为第1层,根节点的子节点为第2层,依此类推,如果某一个节点位于第L层,则其子节点位于第L+1层
- ⑦树的深度:也称为树的高度,树中所有节点的层次最大值称为树的深度
- ⑧有序树:如果树中各棵子树的次序是有先后次序,则称该树为有序树
- ⑨无序树:如果树中各棵子树的次序没有先后次序,则称该树为无序树
- ⑩森林:由m(m≥0)棵互不相交的树构成一片森林,如果把一棵非空的树的根节点删除,则该树就变成了一片森林,森林中的树由原来根节点的各棵子树构成
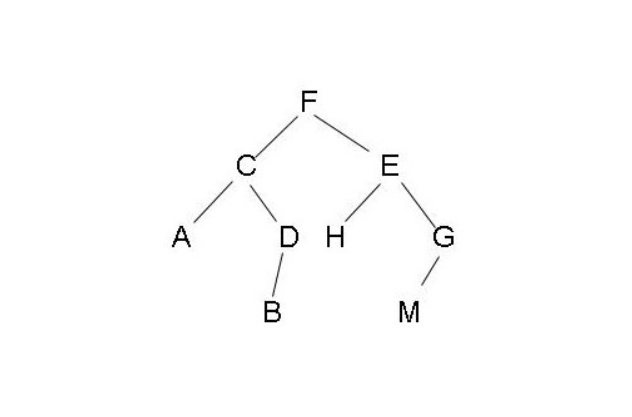
树是一种重要的数据结构,其本质作用就是存储信息,接下来我们重点分析红黑树和它的前身,体会它们的优劣势
二叉查找树-BST
二叉查找树(Binary Search Tree)又称为二叉排序树,二叉搜索树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有结点的值都小于根结点的值
- 若它的右子树不为空,则右子树上所有结点的值都大于根结点的值
- 它的左右子树也分别是二叉搜索树
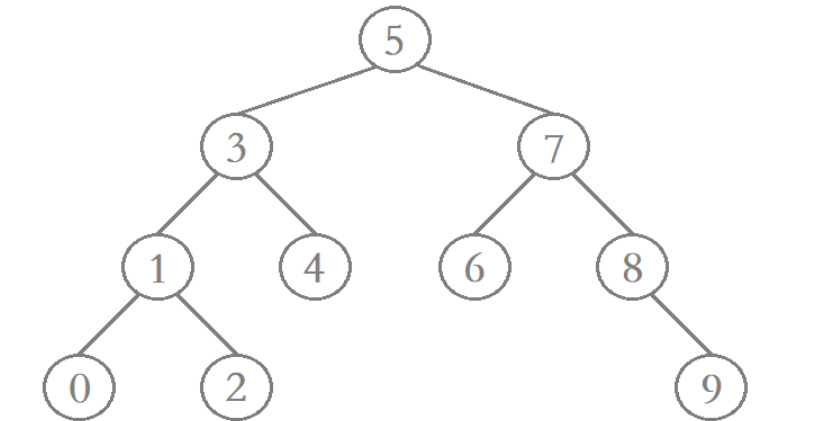
这种树最大的特点就是:左边结点 < key < 右边结点(子结点也是这样的性质)
在查找某个数据 m 时,就可以通过对比 key 与 m 的大小,来判断到底去左结点还是右结点,这种基于二分法的查找方式大大提高了效率
但二叉查找树也有它的缺点,先看以下例子:
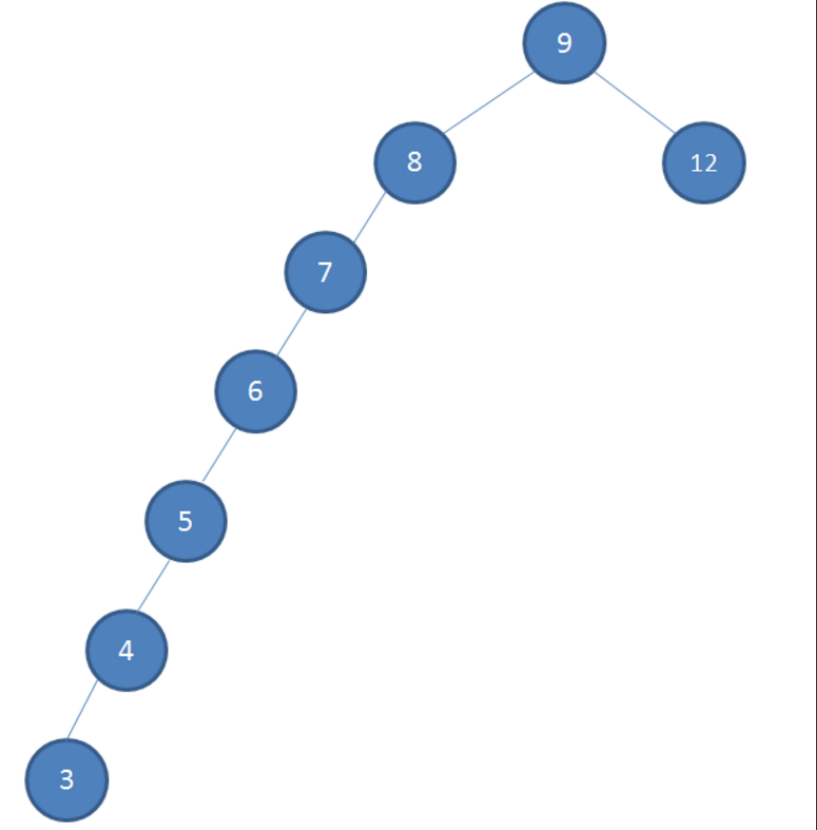
依次插入:7,6,5,4,3,由于每一次插入的值都比对应的 key 小,所以这些数据都会插入树的左结点,发挥不出树的查找优势了(使树“退化”为链表)
这个问题的本质就是:树的左右两边不平衡
平衡二叉树就是用于解决这个问题的,而实现平衡的算法多种多样,就是效率有差别,接下来分析几个平衡算法
二叉平衡搜索树-AVL
二叉平衡搜索树是最早被发明的自平衡二叉查找树,由前苏联的数学家 Adelse-Velskil 和 Landis 在 1962 年提出的高度平衡的二叉树,根据科学家的英文名也称为 AVL 树
它具有如下几个性质:
- 可以是空树
- 假如不是空树,任何一个结点的左子树与右子树都是平衡二叉树
- 所有结点平衡因子的绝对值都不超过 1
- 平衡因子:左子树高度 - 右子树高度
下图,新插入节点 37,该树不再是平衡二叉树,因为,节点 58 的左右子树高度差为 2:
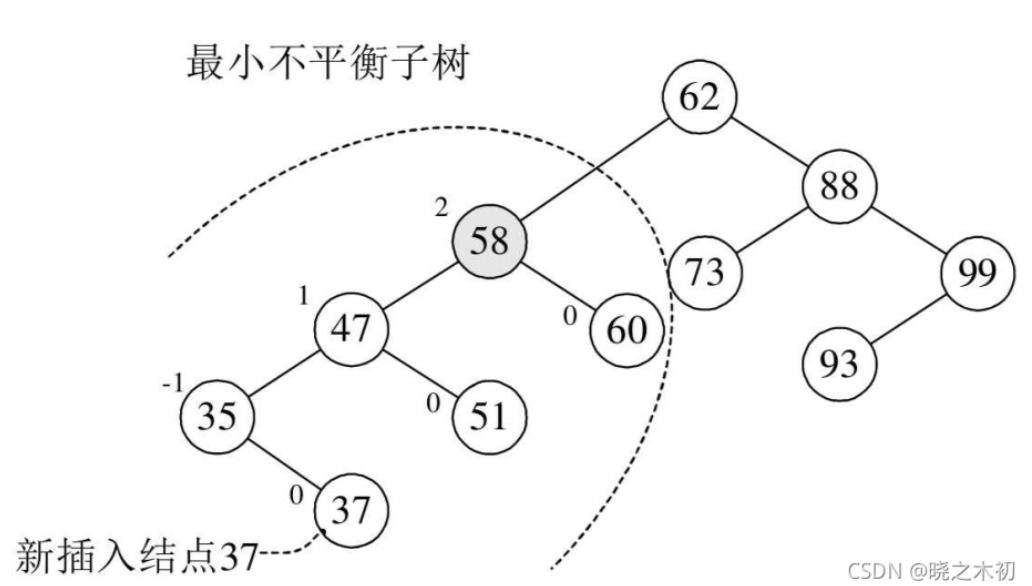
为了使该树重新变为平衡二叉树,需要用到 平衡二叉树的左旋/右旋
右旋:将根节点绕左儿子 顺时针下压
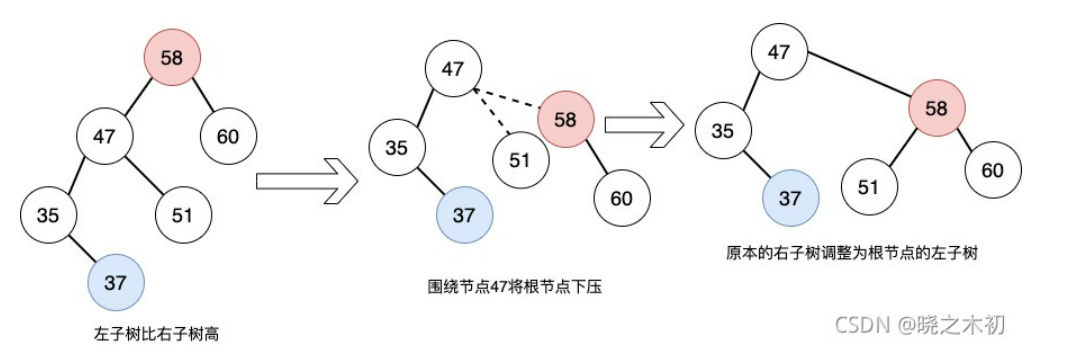
左旋:将根节点绕右儿子 逆时针下压
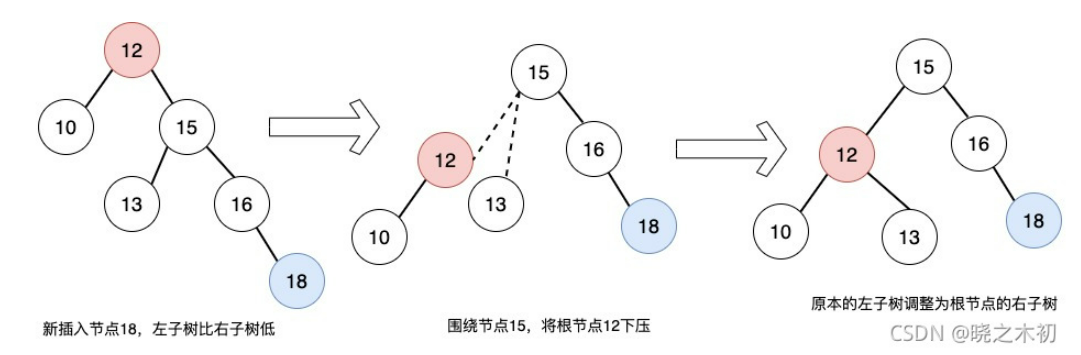
最后就该考虑:什么时候使用左旋,什么时候使用右旋
为此,需要判断调整的四种情况:
- LL:新插入节点为最小不平衡子树根节点的左儿子的左子树上 → 右旋使其恢复平衡
- RR:新插入节点为最小不平衡子树根节点的右儿子的右子树上 → 左旋使其恢复平衡
- LR:新插入节点为最小不平衡子树根节点的左儿子的右子树上 → 以左儿子为根节点进行左旋,再按原始的根节点右旋
- RL:新插入节点为最小不平衡子树根节点的右儿子的左子树上 → 以右儿子为根节点进行右旋,再按原始的根节点左旋
B树-B
B-树是一种平衡的多路查找树
- 注意:B树就是B-树,”-“是个连字符号,不是减号
我们假设我们的数据量达到了亿级别,主存当中根本存储不下,我们只能以块的形式从磁盘读取数据,与主存的访问时间相比,磁盘的 I/O 操作相当耗时,而提出 B-树的主要目的就是减少磁盘的 I/O 操作
一颗 m 阶的B树定义如下:
- 每个结点最多有 m-1 个关键字
- 根结点最少可以只有1个关键字
- 非根结点至少有 Math.ceil(m/2)-1 个关键字(Math.ceil:向上取整)
- 每个结点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它
- 所有叶子结点都位于同一层,或者说根结点到每个叶子结点的长度都相同
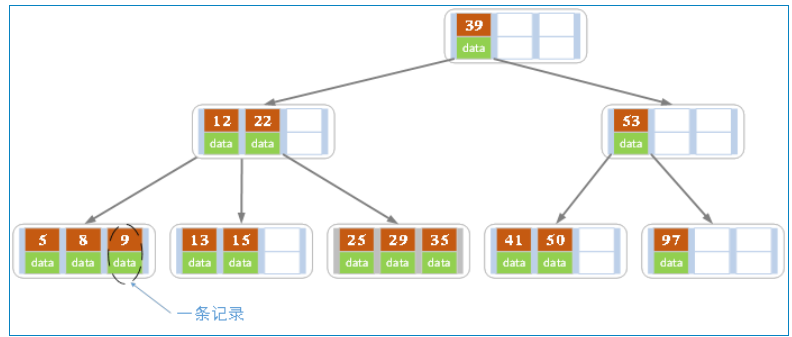
- 上图是一个4阶的B树,所以每个结点最多有3个关键字
- 在实际应用中的B树的阶数 m 都非常大(通常大于100),所以即使存储大量的数据,B树的高度仍然比较小
- 一个 key 和其对应的 data 称为一个记录,即键值对(key, value)
B树,插入操作:
插入操作是指插入一条记录,即(key, value)的键值对,如果B树中已存在需要插入的键值对,则用需要插入的 value 替换旧的 value,若B树不存在这个 key,则一定是在叶子结点中进行插入操作
- 根据要插入的 key 的值,找到叶子结点并插入
- 断当前结点 key 的个数是否小于等于 m-1,若满足则结束,否则进行第3步
- 以结点中间的 key 为中心分裂成左右两部分,然后将这个中间的 key 插入到父结点中, 这个 key 的左子树指向分裂后的左半部分,这个 key 的右子支指向分裂后的右半部分,然后将当前结点指向父结点 ,继续进行第3步
案例如下:
1 | 22 <-> 39 <-> 41 <-> 97 |
1 | 22 <-> 39 <-> 41 <-> 53 <-> 97 /* 插入后超过了最大允许的关键字个数4 */ |
1 | 41 |
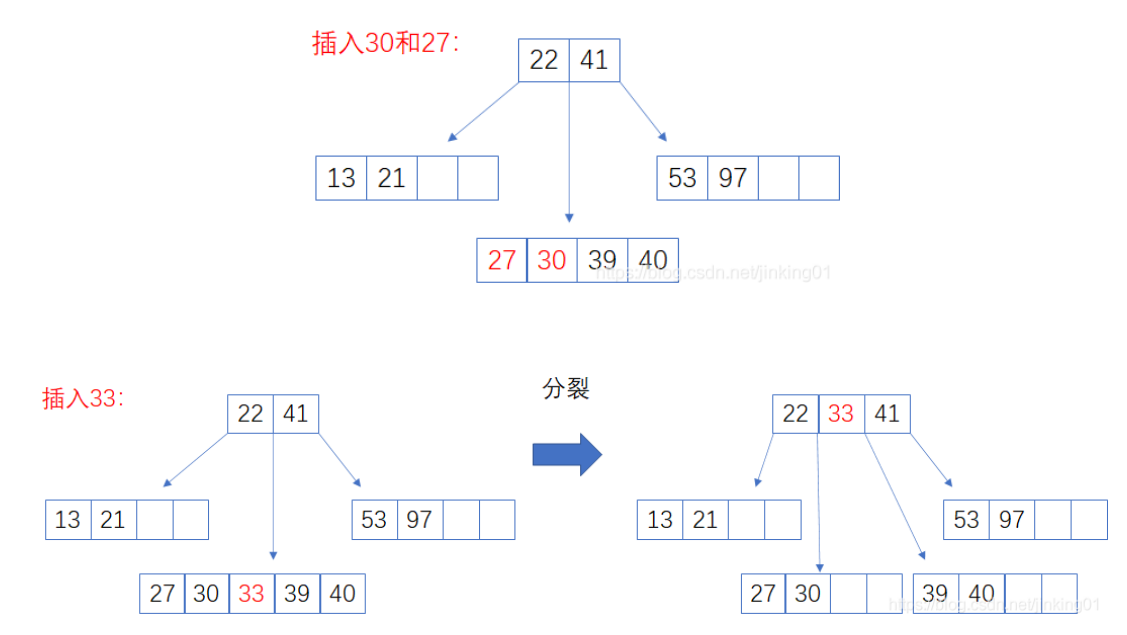
- 这个 key 的左子树指向分裂后的左半部分
- 这个 key 的右子支指向分裂后的右半部分
- 然后将当前结点指向父结点
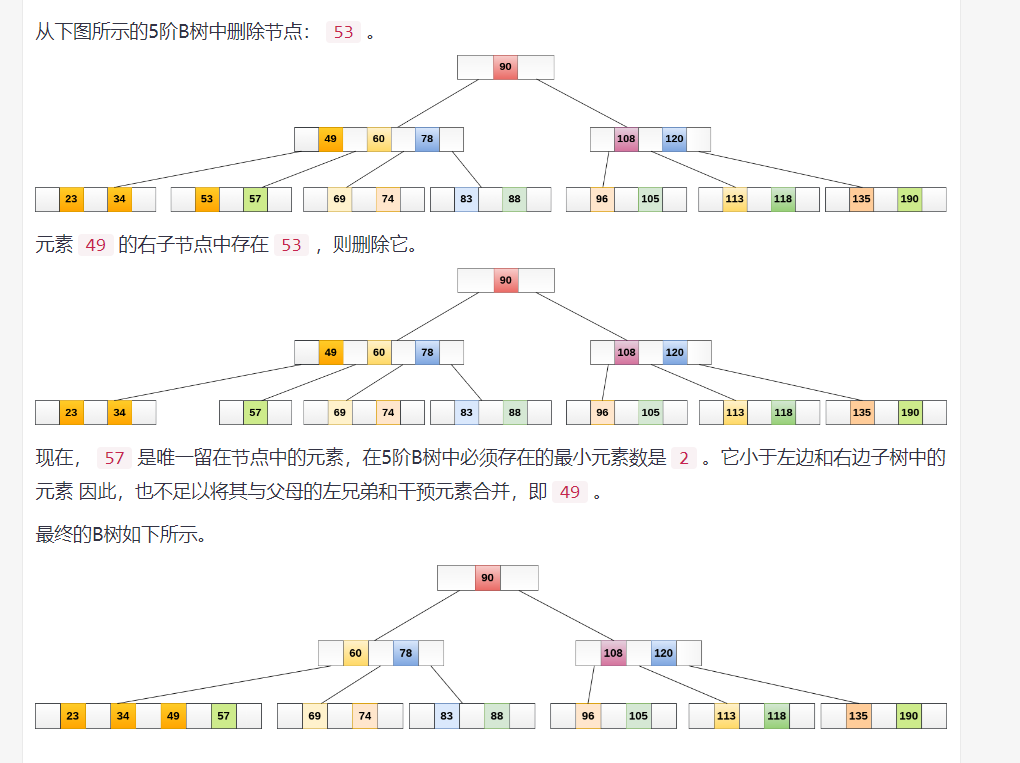
B树,删除操作:
删除操作是指,根据 key 删除记录,如果B树中的记录中不存对应 key 的记录,则删除失败
- 找到叶节点
- 如果叶节点中有多于
m//2个键,则从节点中删除所需的键 - 如果叶节点不多于
m//2个键,则通过从8个或左兄弟中获取元素来完成键- 如果左侧兄弟包含多于
m//2个元素,则将其最大元素推送到其父元素,并将插入元素向下移动到删除键的节点 - 如果右侧兄弟包含多于
m//2个元素,则将其最小元素向上推送到父节点,并将插入元素向下移动到删除键的节点
- 如果左侧兄弟包含多于
- 如果兄弟节点都不包含多于
m//2个元素,则通过连接两个叶节点和父节点的插入元素来创建新的叶节点 - 如果父节点的节点少于
m//2,那么也应在父节点上应用上述过程 - 如果要删除的节点是内部节点,则将节点替换为其有序后继或前一个节点,由于后继或前任将始终位于叶节点上,因此该过程将类似于从叶节点中删除节点
- 总之叶节点不能少于
m//2个键 - 如果少于,则把该父结点以及它的所有子结点 重新整合 到其他结点上
234树-234
2-3-4树是4阶的B树,它被称为2-3-4树,因为非叶非根节点的子节点数为 2, 3 或 4,同时,2-3-4树也是红黑树的前身
2-3-4树的特点:
- 它是平衡树
- 每个节点最多可以存三个数据项
- 不存在空节点
- 叶节点可以有数据项没有子节点
- 插入数据项的时候数据总是插入在叶节点中(这点很重要)
- 对于非叶节点来说:
- 有一个数据项的节点总是有两个子节点
- 有两个数据项的节点总是有三个子节点
- 有三个数据项的节点总是有四个子节点
- L:表示子节点个数
- D:表示数据项个数
- 针对非叶节点:L = D+1
- 子节点个数=数据项个数+1
红黑树
红黑树是对概念模型2-3-4树的一种实现,由于直接进行不同节点间的转化会造成较大的开销,所以选择以二叉树为基础,在二叉树的属性中加入一个 颜色属性 来表示2-3-4树中不同的节点
红黑规则:
- 节点不是黑色,就是红色(非黑即红)
- 根节点为黑色,叶节点为黑色(叶节点是指末梢的空节点
Nil或Null) - 一个节点为红色,则其两个子节点必须是黑色的(根到叶子的所有路径,不可能存在两个连续的红色节点)
- 每个节点到叶子节点的所有路径,都包含相同数目的黑色节点(相同的黑色高度)
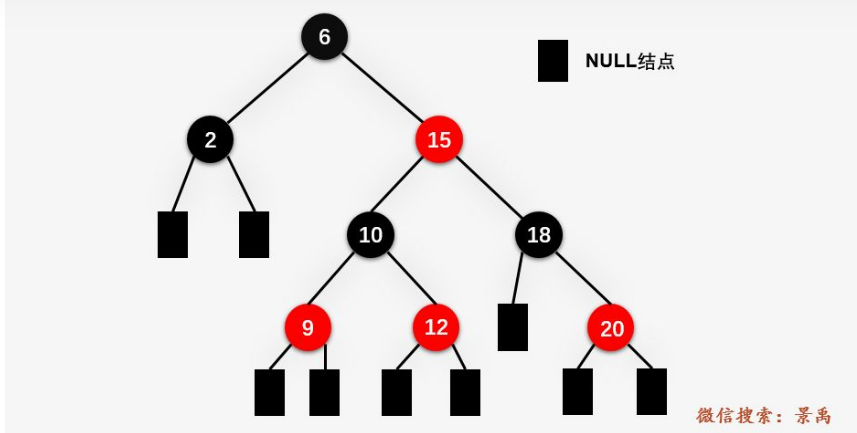
- 4个规则必须全部符合,就构成了红黑树
在插链的过程中,可能会破坏这些规则,这就需要一些机制来恢复平衡
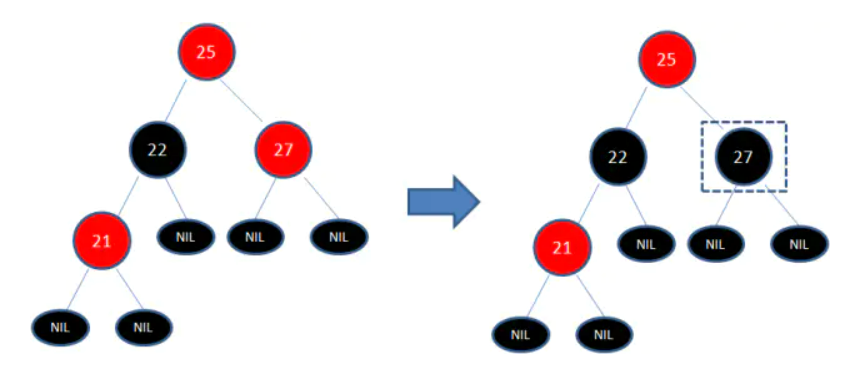
变色:
- 为了重新符合红黑树的规则,尝试把红色节点变为黑色,或者把黑色节点变为红色
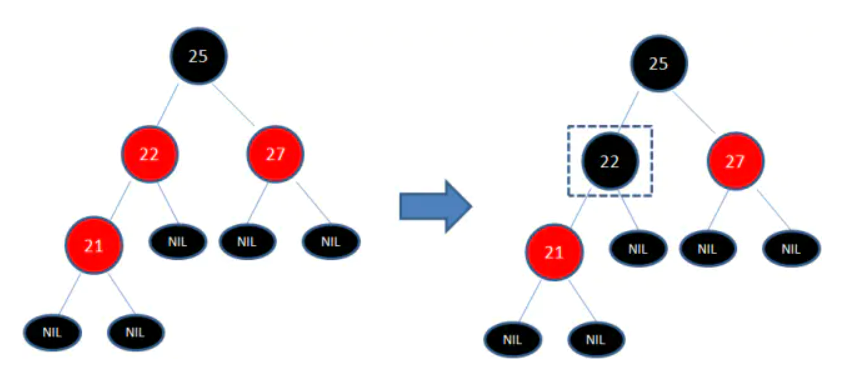
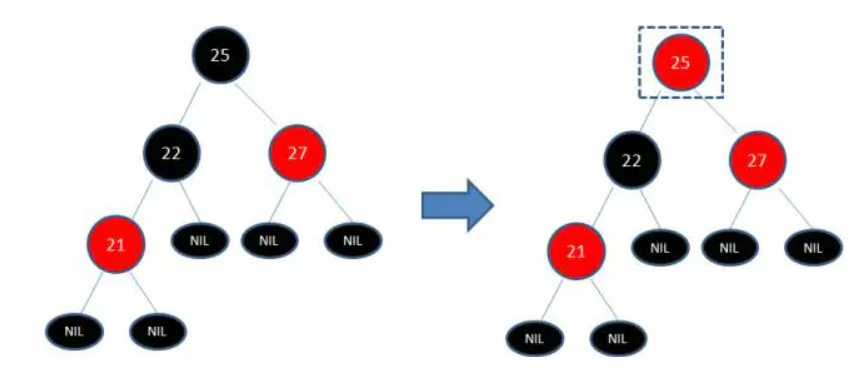
左旋转:
- 左旋转,就是将S点旋转到根节点,S节点的左边都挂到E节点的右边
- 就是将要旋转的子结点的左边挂到之前节点E的右边
右旋转:
- 将要旋转的子结点的右边移到之前结点E的左边

总结:
