Machine-Learning-Lab5

实验介绍

在本练习中，您将实现正则化线性回归，并使用它来研究具有不同偏差-方差特性的模型

• ex5.m - Octave/MATLAB脚本，帮助您完成练习
• ex5data1.mat - 数据集
• submit.m - 将您的解决方案发送到我们的服务器
• featureNormalize.m - 标准化函数
• fmincg.m - 拟合函数，最小化例程（类似于fminunc）
• plotFit.m - 绘制多项式拟合图
• trainLinearReg.m - 使用 fmincg 训练线性回归（代价函数为：均方误差）
• [?] linearRegCostFunction.m - 正则线性回归代价函数
• [?] learningCurve.m - 生成学习曲线
• [?] polyFeatures.m - 将数据映射到多项式特征空间
• [?] validationCurve.m - 生成交叉验证曲线

Regularized Linear Regression（正则线性回归）

在本练习的前半部分，您将使用正则化线性回归，利用水库水位的变化来预测流出大坝的水量，在下半部分中，您将完成一些调试学习算法的诊断，并检查偏差与方差的影响

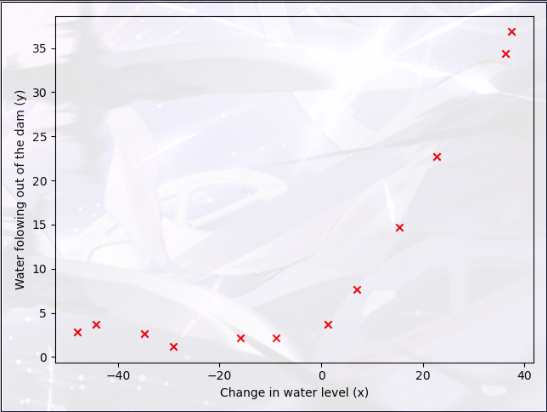
Visualizing the dataset（可视化数据集）

首先，我们将可视化数据集，其中包含：

• 水位变化的历史记录 x
• 流出大坝的水量 y

该数据集分为三个部分：

• 你的模型将学习的训练集：X，y
• 用于确定正则化参数的交叉验证集：Xval，yval
• 用于评估性能的测试集，这些是您的模型在培训期间没有看到的“看不见的”示例：Xtest、ytest

代码实现：

# ============================== 1.读取并显示数据 ==============================
data = scio.loadmat('data\ex5data1.mat')
# 用于训练模型
X = data['X']
Y = data['y'].flatten()
# 用于确定正则化参数的交叉验证
Xval = data['Xval']
Yval = data['yval'].flatten()
# 用于评估性能
Xtest = data['Xtest']
Ytest = data['ytest'].flatten()

plt.figure(1)
plt.scatter(X,Y,c='r',marker='x') # 只显示"用于训练模型"的数据
plt.xlabel('Change in water level (x)')
plt.ylabel('Water folowing out of the dam (y)')
plt.show()

Regularized linear regression cost function（正则线性回归代价函数）

先看下正则化均方误差的公式：

$$J(θ)=\frac1{2m}[\sum_{i=1}^m(h_θ(x^{(i)})−y^{(i)})^2+λ\sum_{j=1}^nθ_j^{2}]$$

• 其中 λ 是控制正则化程度的正则化参数（因此，有助于防止过度拟合）
• 正则化项对总成本 J(θ) 施加惩罚，随着模型参数 θ 的大小增加，惩罚也增加
• 注意：不应该正则化θ0项（在 Octave/MATLAB 中，θ0 项表示为 θ(1) ，因为 Octave/MATLAB 中的索引从1开始）

相应地，正则化线性回归的代价对 θj 的偏导数定义为：

$$\frac{∂J(θ)}{∂θ_0}=\frac{1}{m}\sum_{i=1}^{m}(h_θ(x^{(i)})-y^{(i)})x_{j}^{(i)}\quad for\,\,j=0\\ \frac{∂J(θ)}{∂θ_0}=(\frac{1}{m}\sum_{i=1}^{m}(h_θ(x^{(i)})-y^{(i)})x_{j}^{(i)})+\frac{λ}{m}θ_j\quad for\,\,j>0$$

• 注意：导数和梯度是一个概念，求解偏导数，就是求解梯度

现在，您应该完成文件 linearRegCostFunction.m 中的代码，您的任务是编写一个函数来计算正则化线性回归成本函数，如果可能，尝试将代码矢量化，避免编写循环，然后在本函数中添加代码来计算梯度，并返回变量 grad

实现 linearRegCostFunction 函数：正则线性回归代价函数（均方误差）

"""计算线性回归的代价和梯度"""
import numpy as np

def linear_cost_function(X,Y,theta,lmd):
	m = X.shape[0]
	hyp = X.dot(theta) - Y
	grad = np.zeros(theta.shape) 

	cost = ((hyp.T).dot(hyp) + lmd * (theta.T).dot(theta))/(2*m)

	temp = (X.T).dot(hyp)
	grad[0] = temp[0]/ m
	grad[1:] = (temp[1:] + lmd * theta[1:])/m

	return cost,grad

• 就是实现了一下上述公式，和实验二的 cost_Function_Reg 一样

具体过程：

# ============================ 2.计算代价和梯度 ==============================
(m,n)= X.shape
theta = np.ones((n+1))
lmd=1
cost,grad = linear_cost_function(np.column_stack((np.ones(m),X)),Y,theta,lmd)
print('Cost at theta = [1  1]: {:0.6f}\n(this value should be about 303.993192)'.format(cost))
print('Gradient at theta = [1  1]: {}\n(this value should be about [-15.303016  598.250744]'.format(grad))

Fitting linear regression（拟合线性回归）

将在 trainLinearReg.m 中运行代码，来计算 θ 的最佳值（使用 fmincg 拟合代价函数）

• 在这一部分中，我们将正则化参数λ设置为“0”（因为我们目前线性回归的实现是试图拟合二维 θ，所以正则化对如此低维的θ没有明显的帮助）
• 在本练习的后面部分，您将使用带正则化的多项式回归
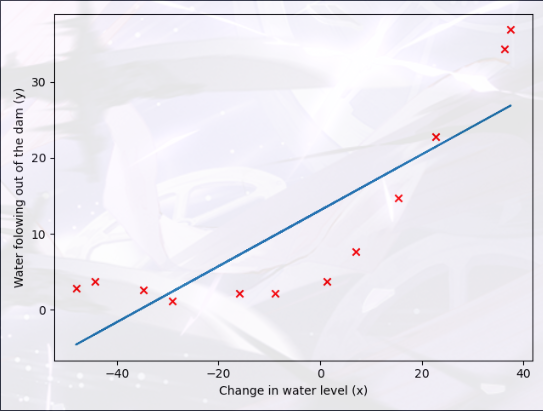
• 最后是 ex5.m 脚本还应绘制最佳拟合线，最佳拟合线会告诉我们：由于数据具有非线性模式，因此模型与数据的拟合度不高
• 虽然可视化显示最佳拟合是调试学习算法的一种可能方法，但可视化数据和模型并不总是容易的，在下一节中，您将实现一个生成学习曲线的函数，该函数可以帮助您调试学习算法，即使数据不容易可视化

实现 trainLinearReg 函数：使用 fmincg 训练线性回归（代价函数为：均方误差）

import numpy as np
from linearCostFunction import linear_cost_function
import scipy.optimize as opt

def train_linear_reg(X,Y,lmd):
	init_theta = np.ones(X.shape[1])

	def cost_func(t):
		return linear_cost_function(X,Y,t,lmd)[0]

	def grad_func(t):
		return linear_cost_function(X,Y,t,lmd)[1]

	theta,*unused = opt.fmin_cg(cost_func,init_theta,grad_func,maxiter=200,disp=False,full_output =True)

	return theta

• 使用 fmincg 进行拟合

具体过程：

# =========================== 3.训练线性回归 ===========================
lmd = 0
theta = train_linear_reg(np.column_stack((np.ones(m),X)),Y,lmd)
plt.plot(X,np.column_stack((np.ones(m),X)).dot(theta))
plt.show()

绘图结果：

Bias-variance（偏差方差）

机器学习中的一个重要概念是：偏差方差

• 具有高偏差的模型对于数据来说不够复杂，并且倾向于欠拟合
• 而具有高方差的模型对训练数据过度拟合

在这部分练习中，您将在学习曲线上绘制训练和测试错误，以诊断 “偏差-方差” 问题

Learning curves A（学习曲线）

现在，您将实现生成学习曲线的代码，这些曲线在调试学习算法时非常有用

• 为了绘制学习曲线，我们需要使用不同的训练集大小进行训练，得出交叉验证的误差（分别得出训练集，测试集的误差）
• 要获得不同的训练集大小，应使用原始训练集X的不同子集，可以使用 trainLinearReg 函数来查找θ参数
• 请注意，lambda 作为参数传递给 learningCurve 函数，在学习θ参数之后，应该计算训练集和交叉验证集的误差

实现 learningCurve 函数：生成学习曲线

import numpy as np

from linearCostFunction import linear_cost_function # 正则线性回归代价函数(均方误差)
from trainLinearRegression import train_linear_reg # 拟合函数fmincg

def learning_curve(X,Y,Xval,Yval,lmd):
	m = X.shape[0]
	error_train = np.zeros(m)
	error_val = np.zeros(m)

	for num in range(m):
		theta = train_linear_reg(X[0:num+1,:],Y[0:num+1],lmd) # 使用fmincg训练模型

		error_train[num],_ = linear_cost_function(X[0:num+1,:],Y[0:num+1],theta,lmd) # 获取训练集的cost代价
		error_val[num],_ = linear_cost_function(Xval,Yval,theta,lmd) # 获取测试集的cost代价

	return error_train,error_val

• zeros()：返回来一个给定形状和类型的，用“0”填充的数组

具体过程：

# =========================== 4.线性回归的学习曲线 ==============
lmd = 0 # 不包括正则化项
error_train,error_val = learning_curve(np.column_stack((np.ones(m),X)),Y,
						np.column_stack((np.ones(Yval.size),Xval)),Yval,lmd)
plt.figure(2)
plt.plot(range(m),error_train,range(m),error_val)
plt.title('Learning Curve for Linear Regression')
plt.legend(['Train', 'Cross Validation'])
plt.xlabel('Number of Training Examples')
plt.ylabel('Error')
plt.axis([0, 13, 0, 150])
plt.show()

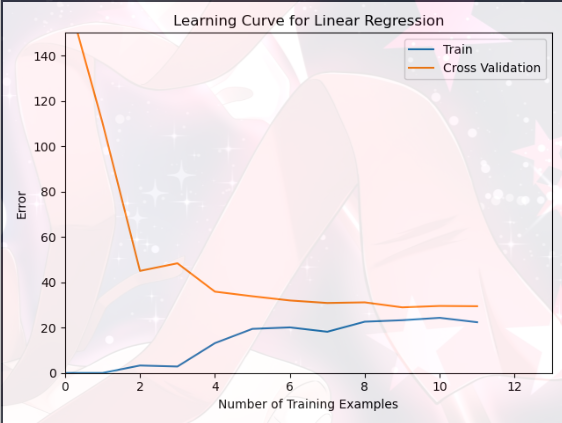
• 注意：这里直接用“代价”来表示“误差”，其实它们两个本来就是同一个概念（反正它们都是用同一个公式计算出来的）

• 随着训练集数目m的增大，训练集和测试集的误差都逐渐趋于平缓，证明模型欠拟合

Polynomial regression（多项式回归）

我们的线性模型的问题是，它对数据来说太简单，导致拟合不足（高偏差）

在本练习的这一部分中，您将通过添加更多功能来解决此问题，对于多项式回归，我们的假设有以下形式：

$$hθ(x)=θ_0+θ_1(waterLevel)+θ_2(waterLevel)^2+ ... +θ_p(waterLevel)^p\\$$ $$hθ(x)=θ_0+θ_1x_1+θ_2x_2+ ... +θ_px_p$$

现在，您将使用“更高的x次方”这一方式（第一个公式），在数据集中添加更多功能，这一部分的任务是完成 polyFeatures 中的代码

实现 polyFeatures 函数：将数据映射到多项式特征空间

import numpy as np

def ploy_feature(X,p):
	m = X.shape[0] # 读取矩阵的长度,("shape[0]"就是读取矩阵第一维度的长度)
	X_poly = np.zeros((m,p)) # 添加更多特征

	for num in range(1,p+1):
		X_poly[:,num-1] = X.flatten() ** num # 添加"次方项"

	return X_poly

• 先对矩阵 X 进行“扩充”，然后提高对应特征的次方（姑且这么理解）

实现 featureNormalize 函数：把数据特征标准化

import numpy as np

def feature_nomalize(X):
	mu = np.mean(X,0) # 计算每一维度的均值
	sigma = np.std(X,0,ddof=1) # 计算沿指定轴的标准差
	X_norm = (X - mu)/sigma

	return X_norm,mu,sigma

• 从数据集中减去每个特征的平均值
• 减去平均值后，再将特征值按各自的“标准偏差”进行缩放（除）

具体过程：

# =============================== 5.投影特征为多项式 ================
p = 8
# 投影和标准化训练集
X_poly = ploy_feature(X,p)
X_poly,mu,sigma = feature_nomalize(X_poly)
X_poly = np.column_stack((np.ones(Y.size),X_poly)) # 将一维数组作为列堆叠到二维数组中

# 投影和标准化验证集
X_poly_val = ploy_feature(Xval,p)
X_poly_val -= mu
X_poly_val /= sigma
X_poly_val = np.column_stack((np.ones(Yval.size),X_poly_val))

# 投影和标准化测试集
X_poly_test = ploy_feature(Xtest,p)
X_poly_test -= mu
X_poly_test /= sigma
X_poly_test = np.column_stack((np.ones(Ytest.size),X_poly_test))

print('Normalized Training Example 1 : \n{}'.format(X_poly[0]))

Learning curves B（学习曲线）

然后我们利用标准化的多项式数据来绘制学习曲线：

# ======================== 6.多项式特征的学习曲线 ===============
lmd = 0
# 绘制拟合曲线
theta = train_linear_reg(X_poly,Y,lmd) # 拟合函数fmincg 
x_fit,y_fit = plot_fit(np.min(X),np.max(X),mu,sigma,theta,p) # 绘制多项式拟合图
plt.figure(3)
plt.scatter(X,Y,c='r',marker='x')
plt.plot(x_fit,y_fit)
plt.xlabel('Change in water level (x)')
plt.ylabel('Water folowing out of the dam (y)')
plt.ylim([-60, 40])
plt.title('Polynomial Regression Fit (lambda = {})'.format(lmd))
plt.show()
# 计算代价误差
error_train, error_val = learning_curve(X_poly, Y, X_poly_val, Yval, lmd)
plt.figure(4)
plt.plot(np.arange(m), error_train, np.arange(m), error_val)
plt.title('Polynomial Regression Learning Curve (lambda = {})'.format(lmd))
plt.legend(['Train', 'Cross Validation'])
plt.xlabel('Number of Training Examples')
plt.ylabel('Error')
plt.axis([0, 13, 0, 150])
plt.show()
print('Polynomial Regression (lambda = {})'.format(lmd))
print('# Training Examples\tTrain Error\t\tCross Validation Error')
for i in range(m):
    print('  \t{}\t\t{}\t{}'.format(i, error_train[i], error_val[i]))

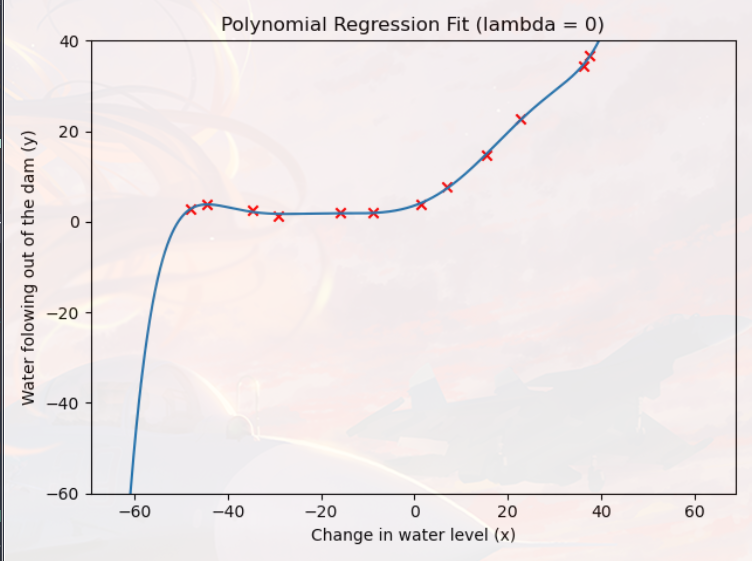
得到两张图片：（lmd = 0，无正则化）

一，拟合曲线（横坐标：水库水位的变化，纵坐标：从大坝流出的水）：

• 您应该看到多项式拟合能够很好地遵循数据点，因此获得了较低的训练误差
• 然而，多项式拟合非常复杂，甚至在极端情况下会下降
• 这是多项式回归模型 过度拟合 训练数据并且不能很好地泛化的指标

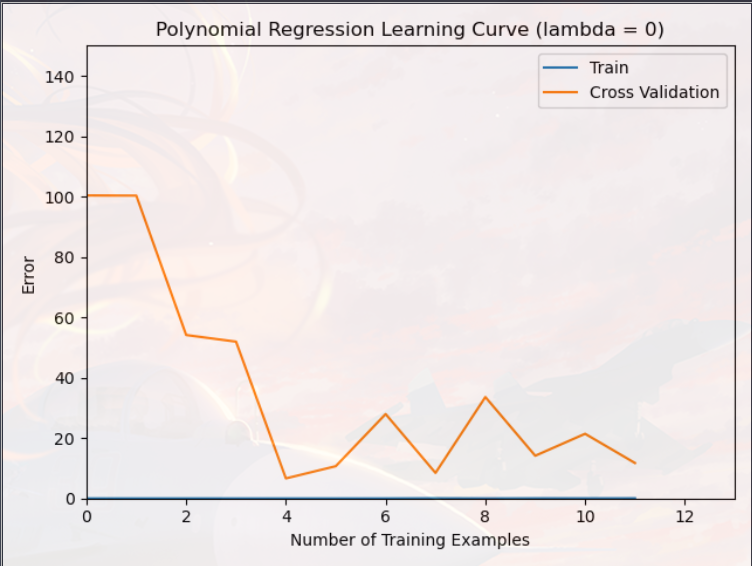
二，学习曲线：

• 注意：蓝线一直在最下面
• 您可以看到学习曲线在低训练误差低但交叉验证误差高的情况下表现出相同的效果
• 训练和交叉验证错误之间存在差距，表明存在高方差问题

Adjusting the regularization parameter（调整正则化参数）

在本节中，您将观察正则化参数如何影响正则化多项式回归的偏差方差（主要是通过正则化来消除过拟合的影响）

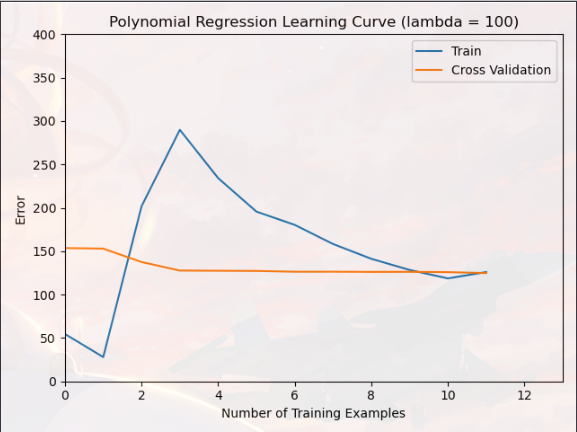
您现在应该修改 ex5.m 中的 lambda 参数并尝试 λ = [1, 100]，对于这些值中的每一个，脚本应该生成适合数据的多项式以及学习曲线

其实就是把上一部分的 “λ=0” 修改为其他值

• lmd = 1：

• lmd = 100：

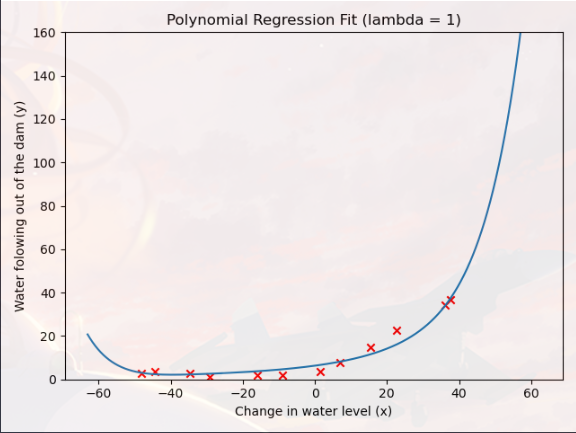
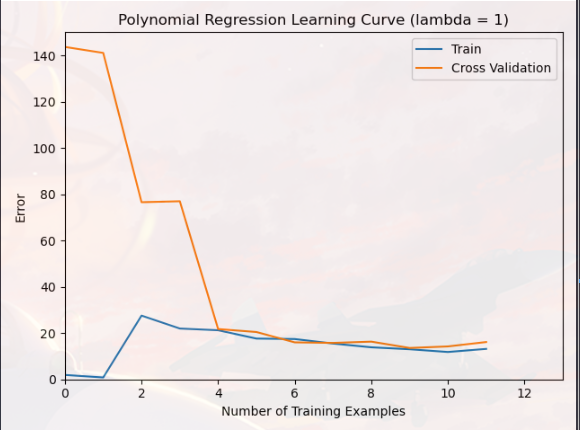
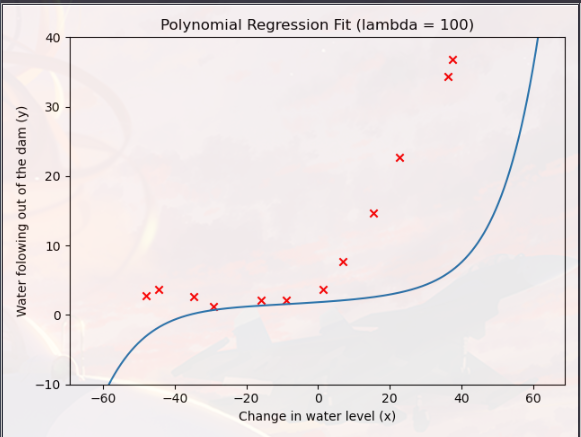
可以对比一下“λ=0”，“λ=1”，“λ=100”，对模型过拟合的影响（明显“λ=1”的模型效果最好）

Selecting λ using a cross validation set（使用交叉验证集选择λ）

从练习的前面部分中，您观察到 λ 的值会显着影响正则化多项式回归，在训练集和交叉验证集上的结果

• 特别是，没有正则化（λ = 0）的模型很好地拟合了训练集，但不能泛化
• 相反，正则化过多（λ = 100）的模型不能很好地拟合训练集和测试集
• 一个好的 λ 选择（λ = 1）可以很好地拟合数据

在本节中，您将实现一个自动方法来选择 λ 参数，具体来说，您将使用交叉验证集来评估每个 λ 值的好坏，在使用交叉验证集选择最佳 λ 值后，我们可以在测试集上评估模型，以估计模型在实际看不见的数据上的表现

您的任务是完成 validationCurve.m 中的代码

• 具体来说，您应该使用 trainLinearReg 函数使用不同的 λ 值训练模型
• 并计算训练误差和交叉验证误差
• 您应该在以下范围内尝试 λ：{0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10}

实现 validationCurve 函数：生成交叉验证曲线

import numpy as np
from linearCostFunction import linear_cost_function
from trainLinearRegression import train_linear_reg

def validation_curve(X,Y,Xval,Yval):
	lambda_vec = np.array([0., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10])
	error_train = np.zeros(lambda_vec.size)
	error_val = np.zeros(lambda_vec.size)

	for num in range(lambda_vec.size):
		lmd = lambda_vec[num]
		theta = train_linear_reg(X,Y,lmd)
		error_train[num],_ = linear_cost_function(X,Y,theta,lmd)
		error_val[num],_ = linear_cost_function(Xval,Yval,theta,lmd)

	return lambda_vec,error_train,error_val

具体过程：

# ============== 7.通过交叉验证集选择正则项系数lambda =========
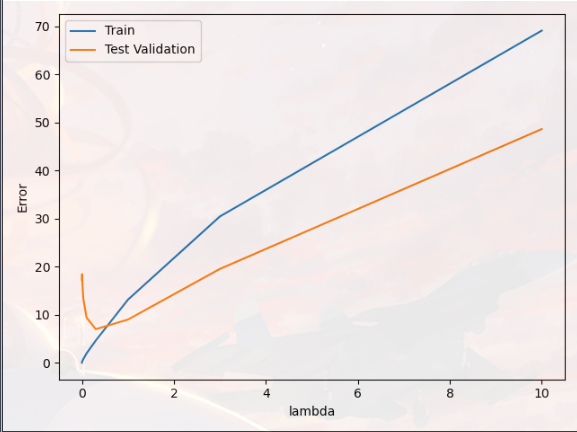
lambda_vec,error_train,error_val = validation_curve(X_poly,Y,X_poly_test,Ytest)
plt.figure(5)
plt.plot(lambda_vec, error_train, lambda_vec, error_val)
plt.legend(['Train', 'Test Validation'])
plt.xlabel('lambda')
plt.ylabel('Error')
plt.show()

绘制图像：

• 我们可以看到 λ 的最佳值在“3”左右（由于数据集的训练和验证拆分的随机性，交叉验证误差有时可能低于训练错误）

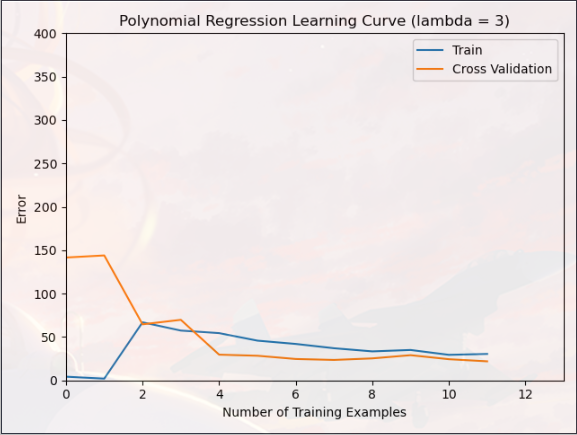
PS：lmd = 3：

可以发现：误差的确比 “lmd=1” 还要小