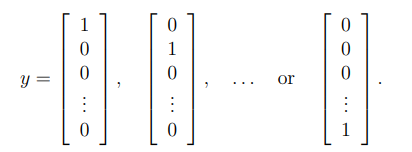Machine-Learning-Lab4

实验介绍

在本练习中，您将实现神经网络的反向传播算法，并将其应用于手写数字识别任务

• ex4.m - Octave/MATLAB 脚本帮助您完成练习
• ex4data1.mat - 手写数字训练集
• ex4weights.mat - 神经网络训练的初始权重
• submit.m - 提交脚本，将您的解决方案发送到我们的服务器
• displayData.m - 帮助可视化数据集的函数
• fmincg.m - 功能最小化例行程序（类似于fminunc）
• sigmoid.m - Sigmoid 函数（假设陈述）
• computeNumericalGradient.m - 计算梯度(倒数)的函数
• checkNNGradients.m - 帮助检查梯度的函数（梯度检测）
• debugInitializeWeights.m - 初始化权重的函数
• predict.m - 神经网络预测函数
• [?] sigmoidGradient.m - 计算sigmoid函数的梯度
• [?] randInitializeWeights.m - 随机初始化权重
• [?] nnCostFunction.m - 神经网络代价函数

Neural Networks（神经网络）

在上一个练习中，您实现了神经网络的前馈传播，并使用它使用我们提供的权重预测手写数字

在本练习中，您将实现反向传播算法来学习神经网络的参数，提供的脚本 ex4.m 将帮助你逐步完成这个练习

这与您在上一个练习中使用的数据集相同，ex3data1.mat中有5000个培训示例：

• 其中每个训练示例是数字的 20x20 像素灰度图像
• 每个像素由一个浮点数表示，表示该位置的灰度强度
• 20×20 的像素网格被“展开”成400维向量，这些训练示例中的每一个都成为我们的数据矩阵X中的一行
• 这给了我们一个 5000×400 的矩阵X，其中每一行都是手写数字图像的训练示例
• 训练集的第二部分是 5000 维向量 y，其中包含训练集的标签
• 为了与 Octave/MATLAB 索引更兼容，在没有零索引的情况下，我们将数字0映射到值10，因此，“0”数字标记为“10”，而数字“1”至“9”按其自然顺序标记为“1”至“9”

Visualizing the data（可视化数据）

绘制的过程和上一个实验一样：

# ==================== 1.读取数据，并显示随机样例 ==============================
data = scio.loadmat('data\ex4data1.mat') # 使用scipy.io中的函数读取mat文件,data的格式是字典

# 根据关键字,分别获得输入数据和输出的真值
X = data['X']
Y = data['y'].flatten()

# 随机取出其中的100个样本,显示结果
m = X.shape[0] # m:矩阵长度
rand_indices = np.random.permutation(range(m)) # 把[0,m-1]的数据随机排序
selected = X[rand_indices[1:100],:] # 排序后取前100个样本
display_data(selected) # 显示手写数字样例(这里不展示了)
plt.show()

绘制的图像：

Model representation（模型表示）

我们的神经网络它有三层——输入层、隐藏层和输出层

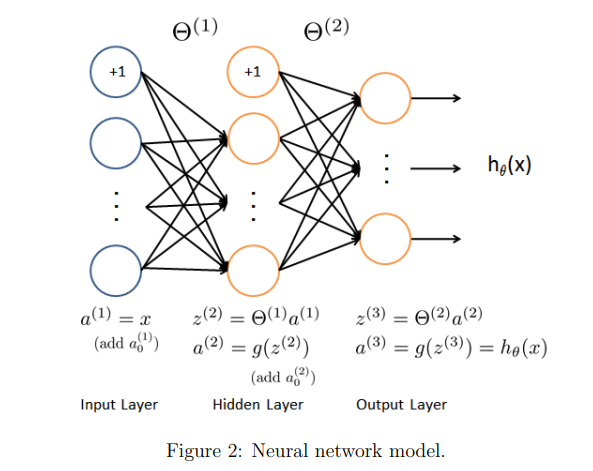
• 我们的输入是3位数图像的像素值，由于图像的大小为 20×20，这给了我们 400 个输入层单元（不包括总是输出+1的额外偏置单元）
• 训练数据将由 ex4.m 脚本加载到变量X和y中
• 我们已经向您提供了一套我们已经培训过的网络参数（θ(1)，θ(2)）这些都存储在 ex4weights.m 中，并将由 ex4.m 加载

Feedforward and cost function（正向传播和代价函数）

现在你将实现神经网络的代价函数和梯度，首先，在 nnCostFunction.m 中完成代码，神经网络的代价函数是：

$$J(θ)=-\frac{1}{m}[\sum_{i=1}^{m}\sum_{k=1}^{K}y_k^{(i)}log(h_θ(x^{(i)}))_k+(1-y_k^{(i)})log(1-(h_θ(x^{(i)}))_k)]+ \frac{λ}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s1}\sum_{j=1}^{s1+1}(θ_{ji}^{(l)})^2$$

这里的 hθ(x) 就可以是逻辑回归中的 Sigmoid 函数（假设陈述），而 θ 就是模型的参数向量（在神经网络中也被称为“权重”）

K=10 是可能标签的总数，注意：虽然原始标签（在变量y中）是 1,2,3……10 为了训练神经网络，我们需要将标签重新编码为只包含值0或1的向量

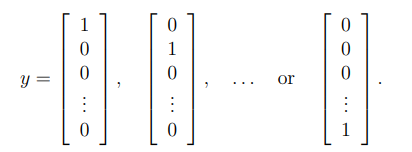
实现过程：

# ==================== 2.读取参数，并计算代价 ==================================
weights = scio.loadmat('data\ex4weights.mat')
theta1 = weights['Theta1']	
theta2 = weights['Theta2']	
nn_paramters = np.concatenate([theta1.flatten(),theta2.flatten()],axis =0) # 把theta1,theta2转化为一维数组后,进行拼接
# 设置参数
input_layer = 400
hidden_layer = 25
out_layer = 10
# 计算代价,无正则项
lmd = 0
cost,grad = nn_cost_function(X,Y,nn_paramters,input_layer,hidden_layer,out_layer,lmd) 
print('Cost at parameters (loaded from ex4weights): {:0.6f}\n(This value should be about 0.287629)'.format(cost))
# 计算代价,带入正则项
lmd = 1
cost,grad = nn_cost_function(X,Y,nn_paramters,input_layer,hidden_layer,out_layer,lmd)
print('Cost at parameters (loaded from ex4weights): {:0.6f}\n(This value should be about 0.383770)'.format(cost))
# 验证sigmoid的梯度
g = sigmoid_gradient(np.array([-1, -0.5, 0, 0.5, 1]))
print('Sigmoid gradient evaluated at [-1  -0.5  0  0.5  1]:\n{}'.format(g))

• flatten()：把数组变成一列的形式，等价于 reshape
• concatenate(a1,a2,…)：能够一次完成多个数组的拼接，其中 a1,a2,… 是数组类型的参数

接下来就分析分析最核心的两个函数：sigmoid_gradient，nn_cost_function

• sigmoid_gradient：计算 sigmoid 函数的梯度（后面会详细分析）

import numpy as np

def sigmoid(z):
	g = 1/(1+np.exp(-z)) # 就是Sigmoid函数
	return g

def sigmoid_gradient(z):
	grad = sigmoid(z) * (1-sigmoid(z))
	return grad

• nn_cost_function：用于计算代价（代价函数-交叉熵）

import numpy as np

from sigmoid import sigmoid
from sigmoid import sigmoid_gradient

def nn_cost_function(X,Y,nn_paramters,input_layer,hidden_layer,out_layer,lmd=0):
    
	theta1 = nn_paramters[:hidden_layer*(input_layer+1)].reshape(hidden_layer,input_layer+1) # 取出theta1
	theta2 = nn_paramters[hidden_layer*(input_layer+1):].reshape(out_layer,hidden_layer+1) # 取出theta2
	m = Y.size # 获取样本数目

	# 输入层的输出等于输入,X增加一列偏置维度
	a1 = np.column_stack((np.ones(X.shape[0]),X)) # 5000*401
	# 隐藏层的输入和输出
	z2 = a1.dot(theta1.T) # 5000*25
	a2 = sigmoid(z2)
	a2 = np.column_stack((np.ones(a2.shape[0]),a2)) # 5000*26
	# 输出层的输入和输出
	z3 = a2.dot(theta2.T) # 5000*10
	a3 = sigmoid(z3) # 5000*10
    
	# a3[m,k]表示第m个样本预测属于k的概率(因为激活函数是logistic函数)
	# 根据Y的值,也转换成和a3相同格式的数组
	# yk中每一行只能有一列值为1,yk[m,k]=1表示第m个样本的真实输出是k,其他列为0
	yk = np.zeros((m,out_layer))
	# 注意:Y中的取值范围是[1,10],而yk中的列下标范围是[0,9]
	for num in range(Y.size):
		yk[num,Y[num]-1] = 1
        
	# 计算代价,因为输出层的激活函数是logistic函数,所有代价也是以logistic regression代价函数
	cost_arr = - yk * np.log(a3) - (1-yk) * np.log(1-a3)
	cost = cost_arr.sum()/m + lmd /(2*m) *( (theta1[:,1:] **2).sum() + (theta2[:,1:] **2).sum())

	# 使用BP算法计算梯度
	delta3 = a3 - yk # 5000*10

	delta2 = delta3.dot(theta2) * sigmoid_gradient(np.column_stack((np.ones(z2.shape[0]),z2)))
	delta2 = delta2[:,1:] # 5000*25
	# theta1的梯度
	theta1_grad = np.zeros(theta1.shape) # 25 x 401
	theta1_grad = theta1_grad + (delta2.T).dot(a1) # 25*401
	nn_parameter1_grad = theta1_grad/m + (lmd/m) * np.column_stack((np.zeros(theta1.shape[0]),theta1[:,1:]))
	# theta2的梯度
	theta2_grad = np.zeros(theta2.shape) # 10 x 26
	theta2_grad = theta2_grad + (delta3.T).dot(a2) # 10*26
	nn_parameter2_grad = theta2_grad/m + (1/m) * np.column_stack((np.zeros(theta2.shape[0]),theta2[:,1:]))
	# 返回梯度
	grad = np.concatenate([nn_parameter1_grad.flatten(),nn_parameter2_grad.flatten()])

	return cost,grad

• 上一个实验是直接导入的 theta1，theta2，而这个实验是用 交叉熵 计算出来的
• 其中包括了反向传播算法（BP算法）来计算梯度，后面会进行分析
• PS：高数和线代太菜了，数学上的理解有点困难，所以我就不折磨自己了

Backpropagation（反向传播）

在这部分练习中，您将实现反向传播算法来计算神经网络代价函数的梯度

• 上一阶段完成的 nnCostFunction.m 会返回一个合适的梯度值（本阶段还会分析一下 nnCostFunction.m 中，使用BP算法计算梯度的那部分）
• 一旦计算出梯度，就可以通过使用先进的优化器 fmincg（类似于fminunc）最小化代价函数 J(θ)，训练神经网络
• 首先，实现反向传播算法来计算（未规范化）神经网络参数的梯度
• 在验证了针对非正则化情况的梯度计算是正确的之后，您将实现正则化神经网络的梯度

Sigmoid gradient（Sigmoid 梯度）

为了帮助您开始这部分练习，您将首先实现 sigmoid gradient 函数，用于计算 Sigmoid 梯度

sigmoid 函数的梯度计算公式为：

$$sigmoid(z)=g(z)=\frac{1}{1+e^{-z}}\\ g^{'}(z)=\frac{d}{d_{z}}g(z)=g(z)(1-g(z))$$

实现代码如下：

import numpy as np

def sigmoid(z):
	g = 1/(1+np.exp(-z)) # 就是Sigmoid函数
	return g

def sigmoid_gradient(z):
	grad = sigmoid(z) * (1-sigmoid(z)) # g(z)=g(z)(1-g(z))
	return grad

Random initialization（随机初始化）

在训练神经网络时，重要的是随机初始化对称性破坏的参数

• 随机初始化的一个有效策略是在范围内均匀地随机选择 θ(l) 的值（范围是：[−init, init]）
• 您应该使用 init(ε)=0.12.2 ，这个值范围确保参数保持较小，并使学习更有效
• 你的工作是完成 randInitializeWeights.m 初始化θ的权重

选择 init 的一个有效策略是基于神经网络中的单元数：

$$ε_{init}=\frac{\sqrt{6}}{\sqrt{L_{in}+L_{out}}}\,\,\,\, (L_{in}=s_l,L_{out}=s_{l+1})\\ PS:s_l和s_{l+1}是相邻层中的单元数$$

实现代码为：

import numpy as np

# 初始化网络参数
def rand_init_weights(L_in,L_out):
	epsilon = np.sqrt(6) / np.sqrt(L_in + L_out)
	init_theta = np.random.random((L_out,L_in+1)) * 2*epsilon - epsilon

	return init_theta

• sqrt(x)：对“x”开平方
• random.random(x,y)：获取一个范围在 [x,y] 的随机浮点数

# =========================== 3.初始化网络参数 =================================
random_theta1 = rand_init_weights(input_layer,hidden_layer) # 初始化网络参数 
random_theta2 = rand_init_weights(hidden_layer,out_layer) # 初始化网络参数
rand_nn_parameters = np.concatenate([random_theta1.flatten(),random_theta2.flatten()]) # 组合后的随机参数(θ集)

lmd =3
check_nn_gradients(lmd) # 梯度检测
debug_cost, _ = nn_cost_function(X,Y,nn_paramters,input_layer,hidden_layer,out_layer,lmd) # 代价函数,用于计算初始代价值
print('Cost at (fixed) debugging parameters (w/ lambda = {}): {:0.6f}\n(for lambda = 3, this value should be about 0.576051)'.format(lmd, debug_cost))

Backpropagation（反向传播的核心算法）

对于反向传播，其实就是进行了如下的一次运算：

$$δ^{(l)}_{j}=a^{(l)}_{j}-y_j$$

• 计算出各个层的 “δ(l,j)”，代表了第 l 层的第 j 结点的误差

计算案例：

$$For\,each\,output\,unit(layer\,\,L=4)\\δ^{(4)}=a^{(4)}-y\\δ^{(3)}=(θ^{(3)})^{T}δ^{(4)}.*g^{'}(z^{(3)})\\δ^{(2)}=(θ^{(3)})^{T}δ^{(3)}.*g^{'}(z^{(2)})$$

• 对于最后一层（输出层），δ4 就是 a4（输出层预测的结果）和 y（真实的结果）之间的差值
• 而对于中间的隐藏层，因为不清楚“预测结果”和“真实结果”的具体值，所以就只能通过以上的公式进行模拟计算

最后，回顾一下“代价函数-交叉熵”的计算过程：

import numpy as np

from sigmoid import sigmoid
from sigmoid import sigmoid_gradient

def nn_cost_function(X,Y,nn_paramters,input_layer,hidden_layer,out_layer,lmd=0):
    
	theta1 = nn_paramters[:hidden_layer*(input_layer+1)].reshape(hidden_layer,input_layer+1) # 取出theta1
	theta2 = nn_paramters[hidden_layer*(input_layer+1):].reshape(out_layer,hidden_layer+1) # 取出theta2
	m = Y.size # 获取样本数目

	# 输入层的输出等于输入,X增加一列偏置维度
	a1 = np.column_stack((np.ones(X.shape[0]),X)) # 5000*401
	# 隐藏层的输入和输出
	z2 = a1.dot(theta1.T) # 5000*25
	a2 = sigmoid(z2)
	a2 = np.column_stack((np.ones(a2.shape[0]),a2)) # 5000*26
	# 输出层的输入和输出
	z3 = a2.dot(theta2.T) # 5000*10
	a3 = sigmoid(z3) # 5000*10
    
	# a3[m,k]表示第m个样本预测属于k的概率(因为激活函数是logistic函数)
	# 根据Y的值,也转换成和a3相同格式的数组
	# yk中每一行只能有一列值为1,yk[m,k]=1表示第m个样本的真实输出是k,其他列为0
	yk = np.zeros((m,out_layer))
	# 注意:Y中的取值范围是[1,10],而yk中的列下标范围是[0,9]
	for num in range(Y.size):
		yk[num,Y[num]-1] = 1
        
	# 计算代价,因为输出层的激活函数是logistic函数,所有代价也是以logistic regression代价函数
	cost_arr = - yk * np.log(a3) - (1-yk) * np.log(1-a3)
	cost = cost_arr.sum()/m + lmd /(2*m) *( (theta1[:,1:] **2).sum() + (theta2[:,1:] **2).sum())

	# 使用BP算法计算梯度
	delta3 = a3 - yk # 5000*10

	delta2 = delta3.dot(theta2) * sigmoid_gradient(np.column_stack((np.ones(z2.shape[0]),z2)))
	delta2 = delta2[:,1:] # 5000*25
	# theta1的梯度
	theta1_grad = np.zeros(theta1.shape) # 25 x 401
	theta1_grad = theta1_grad + (delta2.T).dot(a1) # 25*401
	nn_parameter1_grad = theta1_grad/m + (lmd/m) * np.column_stack((np.zeros(theta1.shape[0]),theta1[:,1:]))
	# theta2的梯度
	theta2_grad = np.zeros(theta2.shape) # 10 x 26
	theta2_grad = theta2_grad + (delta3.T).dot(a2) # 10*26
	nn_parameter2_grad = theta2_grad/m + (1/m) * np.column_stack((np.zeros(theta2.shape[0]),theta2[:,1:]))
	# 返回梯度
	grad = np.concatenate([nn_parameter1_grad.flatten(),nn_parameter2_grad.flatten()])

	return cost,grad

Model Training（模型训练）

代码实现：这里采用 fmincg 来代替梯度下降

# ========================== 4.训练NN ==========================================
lmd = 1
def cost_func(p):
    return nn_cost_function(X,Y,p,input_layer,hidden_layer,out_layer,lmd)[0]

def grad_func(p):
    return nn_cost_function(X,Y,p,input_layer,hidden_layer,out_layer,lmd)[1]

nn_params, *unused = opt.fmin_cg(cost_func, fprime=grad_func, x0=rand_nn_parameters, maxiter=400, disp=True, full_output=True)

# 从返回结果nn_params中获取θ1和θ2(拟合完毕)
theta1 = nn_params[:hidden_layer * (input_layer + 1)].reshape(hidden_layer, input_layer + 1)
theta2 = nn_params[hidden_layer * (input_layer + 1):].reshape(out_layer, hidden_layer + 1)

• fmincg 是一种高效的迭代器，它的需要主要参数依次为：
  • nn_cost_function 返回的代价
  • nn_cost_function 返回的梯度
  • rand_nn_parameters 中存储的随机参数集

Gradient checking（梯度检测）

梯度检测会估计梯度（导数）值，然后和你程序计算出来的梯度的值进行对比，以判断程序算出的梯度值是否正确

公式为：

$$\frac{J(θ_{1}+ε,θ_{2},θ_{3},...,θ_{n})-J(θ_{1}-ε,θ_{2},θ_{3},...,θ_{n})}{2ε}$$

实现过程为：

import numpy as np
import debugInitializeWeights as diw # 初始化权重的函数
import costFunction as ncf # 计算代价的函数
import computeNumericalGradient as cng # 计算梯度(倒数)的函数

def check_nn_gradients(lmd):
    input_layer_size = 3
    hidden_layer_size = 5
    num_labels = 3
    m = 5
    # We generatesome 'random' test data
    theta1 = diw.debug_initialize_weights(hidden_layer_size, input_layer_size)
    theta2 = diw.debug_initialize_weights(num_labels, hidden_layer_size)
    # Reusing debugInitializeWeights to genete X
    X = diw.debug_initialize_weights(m, input_layer_size - 1)
    y = 1 + np.mod(np.arange(1, m + 1), num_labels)
    # Unroll parameters
    nn_params = np.concatenate([theta1.flatten(), theta2.flatten()]) 
    def cost_func(p):
        return ncf.nn_cost_function(X,y,p, input_layer_size, hidden_layer_size, num_labels, lmd)
    cost, grad = cost_func(nn_params) # 通过我们的"代价函数cost_func"计算梯度
    numgrad = cng.compute_numerial_gradient(cost_func, nn_params) # 直接计算梯度
    print(np.c_[grad, numgrad]) # 打印结果

# 初始化权重的函数  
def debug_initialize_weights(fan_out, fan_in):
    w = np.zeros((fan_out, 1 + fan_in))
    w = np.sin(np.arange(w.size)).reshape(w.shape) / 10
    return w
import numpy as np

# 计算梯度(倒数)的函数
def compute_numerial_gradient(cost_func, theta):
    numgrad = np.zeros(theta.size)
    perturb = np.zeros(theta.size)
    e = 1e-4
    for p in range(theta.size):
        perturb[p] = e
        loss1, grad1 = cost_func(theta - perturb)
        loss2, grad2 = cost_func(theta + perturb)

        numgrad[p] = (loss2 - loss1) / (2 * e)
        perturb[p] = 0
    return numgrad

• 在本实验中，我们只对“lmd=3”进行了梯度检测，检测结果如下：

[[ 0.00901304  0.00901304]
 [ 0.05042745  0.05042745]
 [ 0.05455088  0.05455088]
 [ 0.00852048  0.00852048]
 [ 0.01171933  0.01171933]
 [-0.05760601 -0.05760601]
 [-0.01659828 -0.01659828]
 [ 0.03966983  0.03966983]
 [ 0.00366088  0.00366088]
 [ 0.02471166  0.02471166]
 [-0.03245445 -0.03245445]
 [-0.05978209 -0.05978209]
 [-0.0077655  -0.0077655 ]
 [ 0.02526392  0.02526392]
 [ 0.05947174  0.05947174]
 [ 0.03900152  0.03900152]
 [-0.01206378 -0.01206378]
 [-0.05761021 -0.05761021]
 [-0.04520795 -0.04520795]
 [ 0.0087583   0.0087583 ]
 [ 0.30228635  0.30228635]
 [ 0.16784019  0.20149903]
 [ 0.16341919  0.19979109]
 [ 0.16182059  0.16746539]
 [ 0.13164304  0.10137094]
 [ 0.12980928  0.09145231]
 [ 0.09959317  0.09959317]
 [ 0.06275198  0.08903145]
 [ 0.06814118  0.10771551]
 [ 0.06010838  0.07659312]
 [ 0.03765248  0.01589163]
 [ 0.02937856 -0.01062105]
 [ 0.09693242  0.09693242]
 [ 0.057304    0.07411068]
 [ 0.06636988  0.10599418]
 [ 0.06353249  0.089544  ]
 [ 0.04192228  0.03040615]
 [ 0.02820396 -0.01025194]]

• 左边是用我们的代价函数，计算出来的梯度
• 右边是用数学方法，计算出来的梯度
• 通过对比两者的差值，我们可以大体判断一下该代价函数的效果如何

Visualizing the hidden layer（可视化隐藏层）

理解神经网络学习内容的一种方法是可视化隐藏单元捕获的表示

非正式地说，给定一个特定的隐藏单元，可视化其计算内容的一种方法是找到一个将使其激活的输入“x”

实现如下：

# ======================= 5.可视化系数和预测 ===================================

display_data(theta1[:, 1:]) # 和之前实验使用的display_data一样
plt.show()

pred = predict_nn(X,theta1, theta2) # 预测神经网络
print('Training set accuracy: {}'.format(np.mean(pred == Y)*100)) # 计算该模型的准确度

• 实现的原理简单粗暴，直接把输入层输出的激活值放入 display_data 描述数据
• 注意：上一层输出的激活值，会被当做下一层的输出的数据

import matplotlib.pyplot as plt
import numpy as np

def display_data(x):
	(m,n) = x.shape
	# 设置每个小图例的宽度和高度
	width = np.round(np.sqrt(n)).astype(int)
	height = (n / width).astype(int)

	# 设置图片的行数和列数
	rows = np.floor(np.sqrt(m)).astype(int)
	cols = np.ceil(m / rows).astype(int)

	# 设置图例之间的间隔
	pad = 1

	# 初始化图像数据
	display_array = -np.ones((pad + rows*(height+pad), pad + cols*(width + pad)))

	# 把数据按行和列复制进图像中(10x10的表格)
	current_image = 0
	for j in range(rows):
		for i in range(cols):
			if current_image > m:
				break 
			max_val = np.max(np.abs(x[current_image,:]))
			display_array[pad + j*(height + pad) + np.arange(height),pad + i*(width + pad) + np.arange(width)[:,np.newaxis]] = x[current_image,:].reshape((height,width)) / max_val
			current_image += 1
		if current_image > m :
			break

	# 显示图像
	plt.figure()
	# 设置图像色彩为灰度值，指定图像坐标范围
	plt.imshow(display_array,cmap = 'gray',extent =[-1,1,-1,1])
	plt.axis('off')
	plt.title('Random Seleted Digits')

• 把输入的图像数据X进行重新排列，显示在一个面板 figurePane 中
• 面板中有多个小 imge 用来显示每一行数据

描绘结果如下：