Machine-Learning-Lab3

实验介绍

在本练习中，您将实现一对多逻辑回归和神经网络来识别手写数字

• ex3.m - Octave/MATLAB 脚本帮助您完成第1部分
• ex3 nn.m - Octave/MATLAB 脚本帮助您完成第2部分
• ex3data1.mat - 手写数字训练集
• ex3weights.mat - 神经网络训练的初始权重
• submit.m - 提交脚本，将您的解决方案发送到我们的服务器
• displayData.m - 帮助可视化数据集的函数
• fmincg.m - 功能最小化例行程序（类似于fminunc）
• sigmoid.m - Sigmoid 函数（假设陈述）
• [?] lrCostFunction.m - 逻辑回归成本函数
• [?] oneVsAll.m - 训练一个一对多类分类器
• [?] predictOneVsAll.m - 使用一对多类分类器进行预测
• [?] predict.m - 神经网络预测函数

Multi-class Classification（多类分类）

在本练习中，您将使用逻辑回归和神经网络识别手写数字（从0到9）

• 如今，自动手写数字识别被广泛使用——从识别信封上的邮政编码到识别银行支票上的金额
• 本练习将向您展示如何将所学的方法用于此分类任务
• 在练习的第一部分中，您将扩展以前的逻辑回归实现，并将其应用于 one-vs-all（一对多）分类

ex3data1.mat 中提供了一个数据集包含5000个手写数字训练示例（这个 mat 格式意味着数据已以 Octave/MATLAB 矩阵格式保存，而不是像 csv-file 那样的 ASCII 格式），可以使用 load 命令将这些矩阵直接读入程序，加载后，正确尺寸和值的矩阵将出现在程序的内存中，矩阵将已经命名，因此不需要为它们指定名称

• ex3data1.mat 中有5000个训练示例，每个样例都是一个“手写数字”
• 其中每个训练示例的“手写数字”是20像素乘20像素灰度图像，每个像素由一个浮点数表示，表示该位置的灰度强度
• 20×20 的像素网格被“展开”成400维向量，这些训练示例中的每一个都成为我们的数据矩阵X中的一行
• 这给了我们一个 5000×400 的矩阵X，其中每一行都是“手写数字”图像的训练示例
• 训练集的第二部分是 5000 维向量y，其中包含训练集的标签
• 为了与 Octave/MATLAB 索引更兼容，在没有零索引的情况下，我们将数字0映射到值10，因此，“0”数字标记为“10”，而数字“1”至“9”按其自然顺序标记为“1”至“9”

Visualizing the data（可视化数据）

您将首先可视化训练集的一个子集

• 在 ex3.m 的第1部分：代码从X中随机选择100行，并将这些行传递给 displayData 函数
• 此函数将每行映射到 20x20 像素的灰度图像，并一起显示图像
• 我们已经提供了 displayData 函数，我们鼓励您检查代码，看看它是如何工作的，运行此步骤后，应该会看到一个图像

先看一下 displayData 的实现：

import matplotlib.pyplot as plt
import numpy as np

def display_data(x):
	(m,n) = x.shape
	# 设置每个小图例的宽度和高度
	width = np.round(np.sqrt(n)).astype(int)
	height = (n / width).astype(int)

	# 设置图片的行数和列数
	rows = np.floor(np.sqrt(m)).astype(int)
	cols = np.ceil(m / rows).astype(int)

	# 设置图例之间的间隔
	pad = 1

	# 初始化图像数据
	display_array = -np.ones((pad + rows*(height+pad), pad + cols*(width + pad)))

	# 把数据按行和列复制进图像中(10x10的表格)
	current_image = 0
	for j in range(rows):
		for i in range(cols):
			if current_image > m:
				break 
			max_val = np.max(np.abs(x[current_image,:]))
			display_array[pad + j*(height + pad) + np.arange(height),pad + i*(width + pad) + np.arange(width)[:,np.newaxis]] = x[current_image,:].reshape((height,width)) / max_val
			current_image += 1
		if current_image > m :
			break

	# 显示图像
	plt.figure()
	# 设置图像色彩为灰度值，指定图像坐标范围
	plt.imshow(display_array,cmap = 'gray',extent =[-1,1,-1,1])
	plt.axis('off')
	plt.title('Random Seleted Digits')

• 把输入的图像数据X进行重新排列，显示在一个面板 figurePane 中
• 面板中有多个小 imge 用来显示每一行数据

第一部分的代码：

import numpy as np
import scipy.io as scio
import matplotlib.pyplot as plt

# ====== 1.读取数据和初始化 ======
data = scio.loadmat('data\ex3data1.mat') # 使用scipy.io中的函数读取mat文件,data的格式是字典

# 根据关键字,分别获得输入数据和输出的真值
X = data['X']
Y = data['y']
print(X.shape) 

# 随机取出其中的100个样本,显示结果
m = X.shape[0] # m:矩阵长度
rand_indices = np.random.permutation(range(m)) # 把[0,m-1]的数据随机排序
selected = X[rand_indices[0:100],:] # 排序后取前100个样本
display_data(selected) # 显示手写数字样例
plt.show()

• shape：读取矩阵的长度
• permutation(X)：随机排列一个序列，或者数组

绘制的图像：

Vectorizing Logistic Regression（向量化逻辑回归）

现在我们要根据数据集来训练一个模型，使机器可以识别出这些“手写数字”对应的“真正数字”，这很明显是一个分类问题，并且还是多元分类，每个样本都有 10 种可能性（“0”~“9”）

您将使用多个 one-vs-all 逻辑回归模型来构建多类分类器：

• 因为有10个类，你需要训练10个独立的逻辑回归分类器
• 为了提高培训的效率，确保代码具有良好的矢量化非常重要
• 在本节中，您将实现逻辑回归的向量化版本（该版本不使用任何 for 循环）

其实在之前的实验中我们已经在使用向量化了（利用矩阵乘法来代替循环），这里实验要求使用

首先，我们先回忆一下逻辑回归-代价函数（交叉熵）的矢量版本：

$$J(θ)=-\frac1{m}[\sum_{i=1}^my^{(i)}log\,h_θ(x^{(i)})+(1-y^{(i)})log(1-h_θ(x^{(i)}))]$$

因为需要求和，所以矢量版本的代码肯定有循环，但是向量版本却可以用“矩阵乘法”来替代循环：

代价函数 lr_cost_function：（带有正则化）

def lr_cost_function(X,Y,theta,lmd):
	m = X.shape[0]
	g = sigmoid(X.dot(theta))
	Y = Y.reshape(Y.size)

	cost = (-Y.T).dot(np.log(g)) - ((1-Y).T).dot(np.log(1-g))
	cost = cost /(m) + lmd * (theta.T).dot(theta) / (2*m)
	
	grad = (X.T).dot(g-Y)/ m
	grad[0] = grad[0]
	grad[1:] = grad[1:] + (lmd * theta[1:])/m

	return cost,grad

• PS：和前面 ex2 的 costfunction 相同（因为前面的实验都使用了向量化）

实现主体：

# ====== 2.向量化Logistic Rgression ======

theta_t = np.array([-2, -1, 1, 2])
X_t = np.c_[np.ones(5), np.arange(1, 16).reshape((3, 5)).T/10]
y_t = np.array([1, 0, 1, 0, 1])
lmda_t = 3
cost,grad = lr_cost_function(X_t,y_t,theta_t,lmda_t)
np.set_printoptions(formatter={'float': '{: 0.6f}'.format})
print('Cost: {:0.7f}'.format(cost))
print('Expected cost: 3.734819')
print('Gradients:\n{}'.format(grad))
print('Expected gradients:\n[ 0.146561 -0.548558 0.724722 1.398003]')

• set_printoptions：控制Python中小数的显示精度

One-vs-all Classification（一对多分类）

接下来就要实现多元分类的逻辑回归：

在这部分练习中，您将通过训练多个正则化逻辑回归分类器来实现一对所有分类，每个分类器对应于数据集中的K个类

# ====== 3.训练模型 ======

lmd = 0.01
num_labels = 10 # 每个样本有10种可能
all_theta = one_vs_all(X,Y,num_labels,lmd) # 模型拟合
pred = predict_one_vs_all(X,all_theta) # 预测手写数字
Y = Y.reshape(Y.size) # 这里一定要把Y.shape变成横向量(之前是竖向量)
print('Training set accurayc:{}'.format(np.mean(pred == Y)*100)) # 计算精度

模型拟合的具体过程在 one_vs_all 函数中，看看该函数的代码：

import scipy.optimize as opt
import numpy as np

from sigmoid import sigmoid
from lrCostFunction import lr_cost_function

def one_vs_all(X,Y,num_labels,lmd):
	X = np.c_[np.ones(X.shape[0]),X] # 给数据添加偏置维度
	n = X.shape[1]
	all_theta = np.zeros((num_labels,n)) # 保存所有theta的集合
	for i in range(1,num_labels+1):
		init_theta = np.zeros((n,1));
		y = (Y == i).astype(int) # Y中的值是1~10(代表可能的分类,注意:"10"代表了"0")
		
		def cost_func(t):
			return lr_cost_function(X,y,t,lmd)[0]
		def grad_func(t):
			return lr_cost_function(X,y,t,lmd)[1]

		theta, cost, *unused = opt.fmin_bfgs(f=cost_func, fprime=grad_func, x0=init_theta, maxiter=100, full_output=True, disp=False) # 使用fminunc进行拟合
		all_theta[i-1,:] = theta.T # 保存theta

	return all_theta

最后看一下预测函数 predict_one_vs_all 的实现：

def predict_one_vs_all(X,all_theta):
	m = X.shape[0]
	X = np.c_[np.ones(m),X]
	num_labels = all_theta.shape[0] # 标签数10
	
	# preds[m][k]是第m个样本属于k的概率
	preds = sigmoid(X.dot(all_theta.T))
	P = np.zeros(m)

	for num in range(m):
		# 找到第num行中,与该行最大值相等的列的下标,此时下标的范围是[0,9]
		# label的范围是[1,10],需要把下标的值+1
		# np.where()返回的是一个长度为2的元祖,保存的是满足条件的下标
		# 元组中第一个元素保存的是行下标,第二元素保存的是列下标
		index = np.where(preds[num,:] == np.max(preds[num,:]))
		P[num] = index[0][0].astype(int) + 1

	return P

Neural Networks（神经网络）

在本练习的前一部分中，您实现了多类逻辑回归来识别手写数字，然而，逻辑回归不能形成更复杂的假设，因为它只是一个线性分类器

在这部分练习中，您将使用与之前相同的训练集实现一个神经网络来识别手写数字，神经网络将能够表示形成非线性假设的复杂模型：

• 本次实验，你们将使用我们已经训练过的神经网络的参数
• 您的目标是实现正向传播算法，使用我们的权重进行预测（已经训练好了）
• 在下次的实验中，您将编写学习神经网络参数的反向传播算法

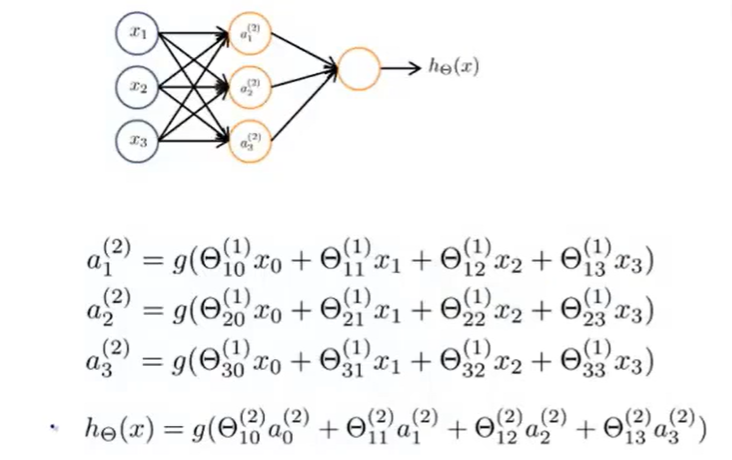
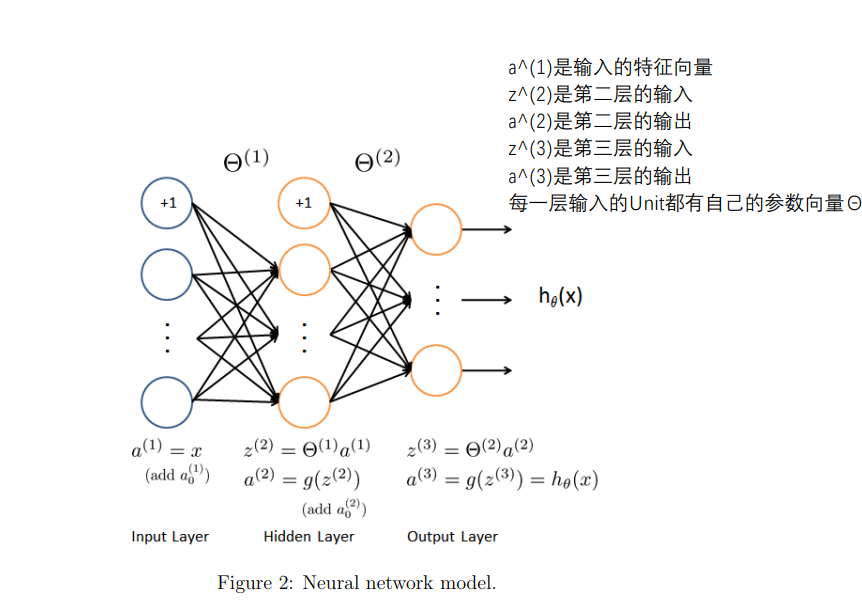
神经网络简图：（具体细节就不解释了）

Model representation（模型表示）

对于本实验的神经网络架构：

这个神经网络有三层：输入层，隐藏层，输出层

• 我们的输入是数字图像的像素值，由于图像的大小为20×20，这给了我们400个输入层单元（不包括总是输出+1的额外偏置单元）
• 与之前一样，训练数据将加载到变量X和y中，我们已经向您提供了一组参数（θ(1),θ(2)），这些参数已经由我们训练过
• 这些都存储在 ex3weights.mat ，并将由 ex3_nn 加载到θ1和θ2，参数的尺寸为神经网络的尺寸，第二层为25个单元，输出为10个单元（对应于10个数字类）

Feedforward Propagation and Prediction（正向传播与预测）

现在，您将为神经网络实现正向传播，您需要在 predict 中完成代码，返回神经网络的预测

你应该实现正向传播算法，为每个示例 i 计算 hθ(x(i)) 并返回相关预测（类似于“一对多”分类策略）

下面是实现过程：

• 1.读取数据，显示随机样例（和上半部分一样）

# ========================= 1.读取数据,显示随机样例 ===========================
data = scio.loadmat('data\ex3data1.mat')
X = data['X']
Y = data['y'].flatten() # 返回一个一维数组
m = X.shape[0] # m:矩阵长度
rand_indices = np.random.permutation(range(m))
selected = X[rand_indices[1:100],:] # 随机取出其中的100个样本
display_data(selected) # 显示手写数字样例
plt.show()

• 2.读取神经网络的参数（）

# ======================= 2.读取神经网络的参数 =================================
weight = scio.loadmat('data\ex3weights.mat')
# 隐藏层有25个节点,输入数据为401维(添加了1个维度的偏置)
# 输出层有10个节点,隐藏层添加一个维度后,有25个输出
theta1 = weight['Theta1']
theta2 = weight['Theta2']

P = predict_nn(X,theta1,theta2) # 预测神经网络
print('Training set accuracy: {}'.format(np.mean(P == Y)*100)) # 计算该模型的准确度

• 3.随机选取样本，并显示预测结果

# ======================= 3.随机选取样本,并显示预测结果 =========================
rp = np.random.permutation(range(m)) # 随机排列一个序列,或者数组
for i in range(m):
    print('Displaying Example image')
    example = X[rp[i]]
    example = example.reshape((1, example.size)) # 调节example为1x1(只有一个方框)
    display_data(example) # 显示手写数字样例
    plt.show()
    
    pred = predict_nn( example,theta1, theta2) # 预测手写数字
    print('Neural network prediction: {} (digit {})'.format(pred, np.mod(pred, 10)))
    s = input('Paused - press ENTER to continue, q + ENTER to exit: ')
    if s == 'q':
        break

• 预测函数 predict_nn 的实现：（有点不理解它为什么要这么组织代码）

# 根据输入的数据和参数，计算神经网络的输出
def predict_nn(X,theta1,theta2):
	m = X.shape[0]
	X= np.c_[np.ones(m),X]
	z1 = theta1.dot(X.T) # 隐藏层的输入
	z1 = np.row_stack((np.ones(z1.shape[1]),z1)) # 增加一行维度
	A1 = sigmoid(z1) # 隐藏层的输出
	z2 = theta2.dot(A1) # 输出层的输入
	A2 = sigmoid(z2.T) # 输出层的输出

	# 进行预测
	P = np.zeros(m)
	for num in range(m):
		# 找到第num行中,与该行最大值相等的列的下标,此时下标的范围是[0,9]
		# label的范围是[1,10],需要把下标的值+1
		# np.where()返回的是一个长度为2的元祖,保存的是满足条件的下标
		# 元组中第一个元素保存的是行下标,第二元素保存的是列下标
		index = np.where(A2[num,:] == np.max(A2[num,:]))
		P[num] = index[0][0].astype(int) + 1

	return P

• where(condition)：满足条件(condition)，输出满足条件元素的坐标
• max(array)：返回 array 的最大值

显示图片：

预期结果：

Neural network prediction: [4.] (digit [4.])